【高校物理】任意の複数の状態を経る熱機関の最大熱効率
任意の2点間ではなく、任意の複数の状態を経由する熱機関の最大熱効率を求めてみます。
各過程の計算
閉鎖系の熱機関に理想気体を封入して、上の任意の点
*1を通過する準静的な可逆過程のみでこれらの点を最小の回数の過程で結ぶサイクルを考えます。任意の2点は断熱過程と等温過程の2過程、または断熱過程、等温過程のいずれか1過程で結ぶことができるので
点を結ぶサイクルは
過程以内で達成することができます。
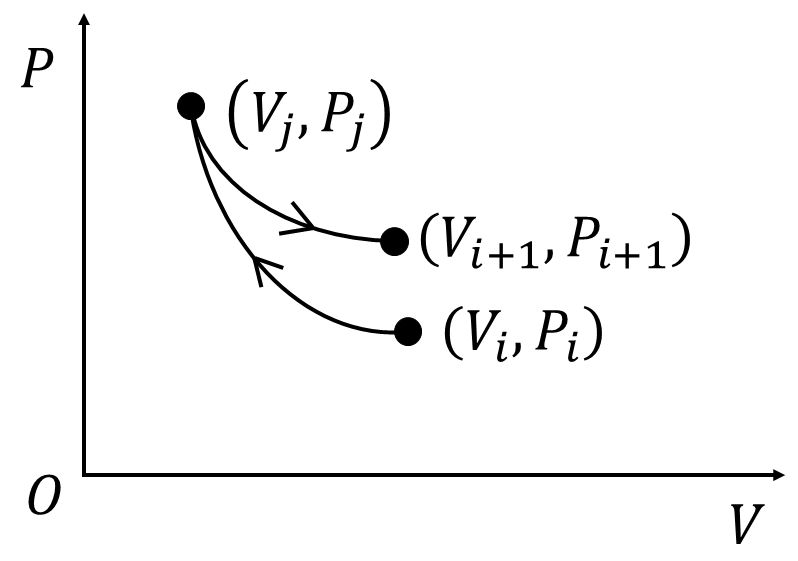
図のようにを経由して
と
を通るときに系が吸収する熱量
を求めます。
は断熱過程、
を等温過程とします。断熱過程のポアソンの法則と等温過程のボイルの法則によって、比熱比
として次の連立方程式が得られます。
を消去し、
が得られます。
断熱過程で熱の出入りはなく、等温過程の吸熱のみを考えればよいため、
熱効率の最大値
上の計算から、点を通るような
過程以内のサイクルの熱効率の最大値
は次のように与えられます。
の引数は断熱過程の保存量の比となっていることがわかります。
*1:原点など物理的に意味のないところは考えていません。